I saw this problem on LeetCode couple of years ago: Longest Palindromic Substring

I used to browse problems on LeetCode every time before I was seeking for a new job. But, you know, it's pretty relaxing. I mean, if I found that i couldn't solve a problem easily, I just gave up. No pressure.

Take this Longest Palindromic Substring for example, I met it a few times before, I knew there is an algorithm called Manacher can solve this. But I've never worked it out even though I knew about the algorithm. Let me try again today.

The first idea came into my head was, find all the palindromic sub-strings and check their lengths. It sounds like crazy but it's actually a viable plan. To make it work, we need to check each character and find out the palindromic sub-string that centered with this character. We can store the "radius" of the palindromic sub-string for each character in the original string, then find out the longest one. So the radius obvious can be 1 or more.

For example, for the character d in string

a b c d c b x

the radius is 3 (d, c, b). For character b, its radius is 1 (only including b itself).

The problem is, for a super long string, calculating the radius for each palindromic string is not efficient. We have to find a way to avoid always accumulating the radius from 1.

The Manacher's algorithm is based on this idea.

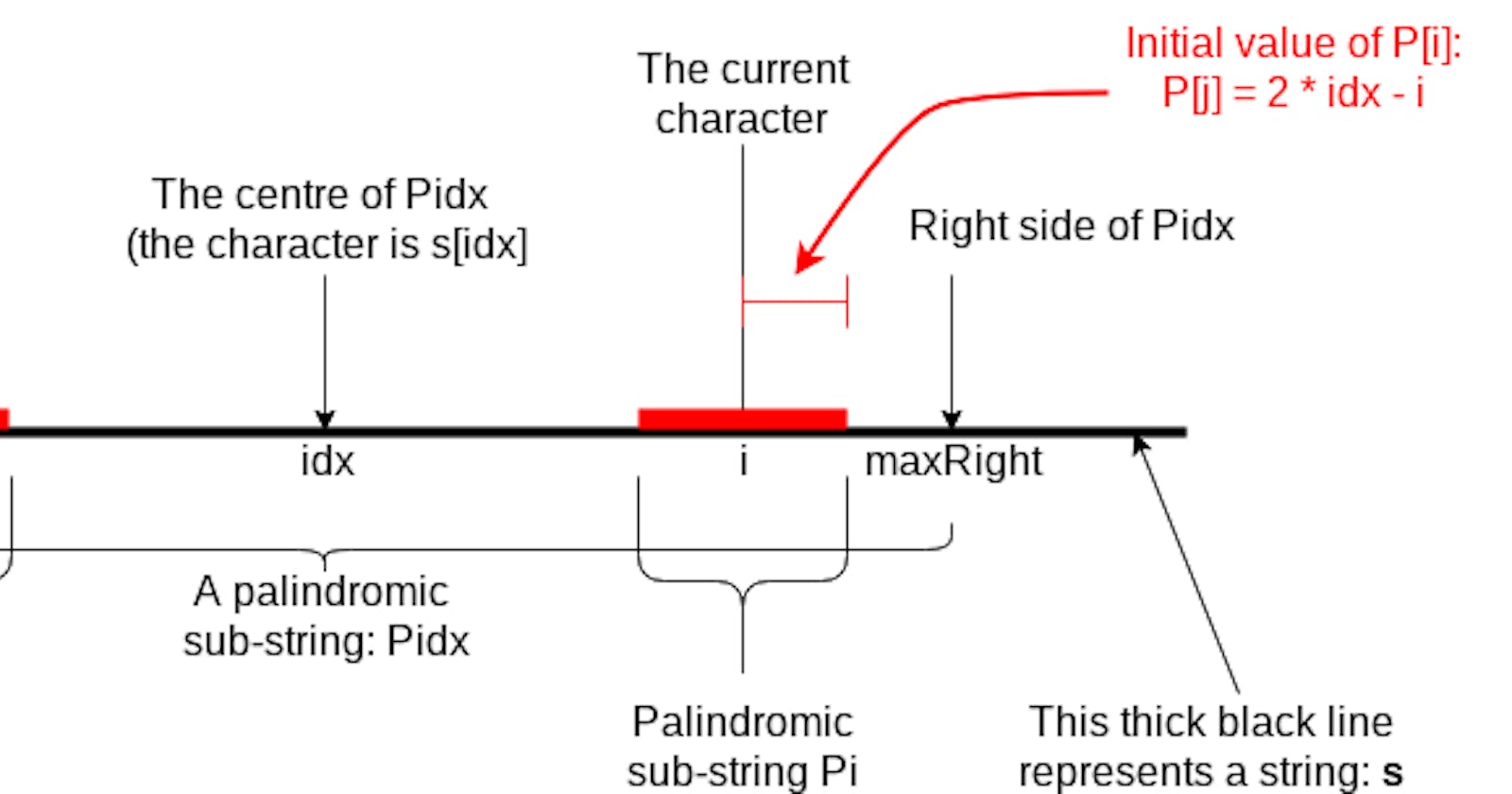
Diagram 1

• We are going to find out the longest palindromic sub-string in a string s
• We go through each character from left to right, and put the radius of the palindromic sub-string (which centered with the current character) into an array P.
• So far the radius (on the right) of the palindromic sub-string with the centre character s[idx] can reach the position maxRight, which is the most right position among all the palindromic sub-strings.
• At the moment we are at the character s[i]. We are going to find the radius of Pi and save it in P[i].

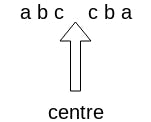
Before we start, we need to handle this issue first: if a palindromic string has even number of characters, the centre of it is a space between two characters

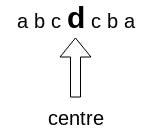
If a string has odd number of character(s), the centre is a character:

So the first step of this Manacher algorithm is, eliminating this ambiguity by inserting an arbitrary character (that doesn't appear in the string), say "#", between every two characters of the string:

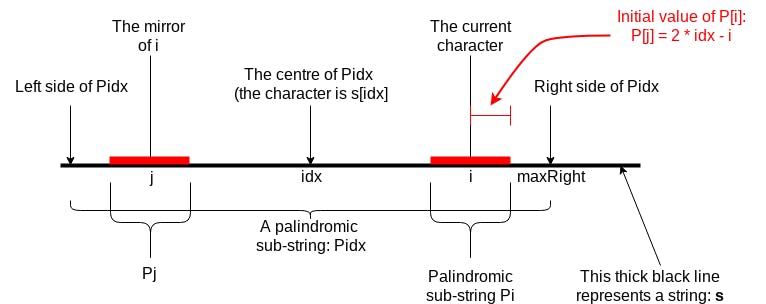
Diagram 2

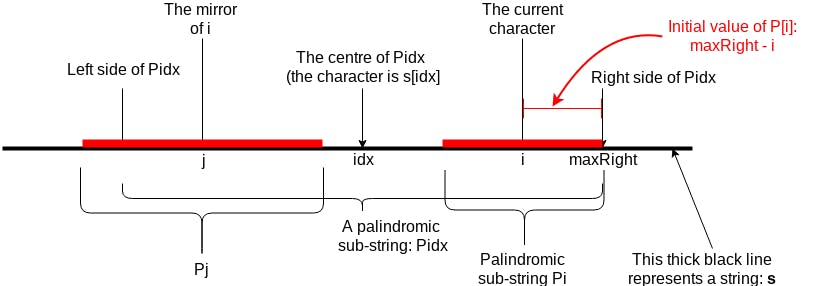
• When i < maxRight, the whole Pi or part of Pi has a "mirror" on the other side of idx. This "mirror" is Pj. Its centre character is s[j].
  • If P[j] is relatively small - the whole Pj is included in Pidx (See Diagram 1): We find the initial value of P[i]. That is, P[i] = P[j]. Then with i as the centre, we expand Pi until it's not palindromic any more or reach the end of s.
  • If P[j] is relatively large - part of Pj is outside Pidx (See Diagram 2): The initial value of P[i] is maxRight - i. Then with i as the centre, we expand Pi until it's not palindromic any more or reach the end of s.
• When i > maxRight, it means there is no history record can be used to calculate Pi, so P[i] will start from 1.

So the critical part of this algorithm: what is the initial value of P[i]? The answer is:

P[i] = min(P[j], maxRight - i);

And here's how to get P[j]: From Diagram 1 we can easily get that idx - j = i - idx, so j = 2 * idx -i.

Now we know the position of the longest palindromic sub-string centre and its radius, so we can get its start position and then work out what this sub-string is. The following code is what I submitted to Leetcode, I'm happy with the 12ms runtime and 10 MB memory used.

class Solution {
public:
    string longestPalindrome(string s) {
        string retStr = s;
        int newLen = s.length() * 2 + 1;

        // First step: Insert "#" to make the string size an odd number
        for (int i = 0; i < newLen; i += 2)
        {
            retStr = retStr.insert(i, "#");
        }
        retStr.insert(0, "$");


        // Process retStr
        vector<int> p(retStr.size(), 0);
        int mx = 0, id = 0, resLen = 0, resCenter = 0;
        for (int i = 1; i < retStr.size(); ++i) {
            p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
            while (retStr[i + p[i]] == retStr[i - p[i]]) ++p[i];
            if (mx < i + p[i]) {
                mx = i + p[i];
                id = i;
            }
            if (resLen < p[i]) {
                resLen = p[i];
                resCenter = i;
            }
        }
        return s.substr((resCenter - resLen) / 2, resLen - 1);
    }
};